Using Machine Learning to find Ambiguous Handwritten Digits

We used to think that computers could only answer math problems, but they have come a long way since then. Computers have moved beyond just understanding text to also understanding images.

This report will guide you through how we can answer the question of “What are the most ambiguous handwritten numbers in a dataset?” As it is clear there is no objective measure of ambiguity (it cannot be given a score out of 10), we will need to use machine learning to transfer this higher-level concept to code.

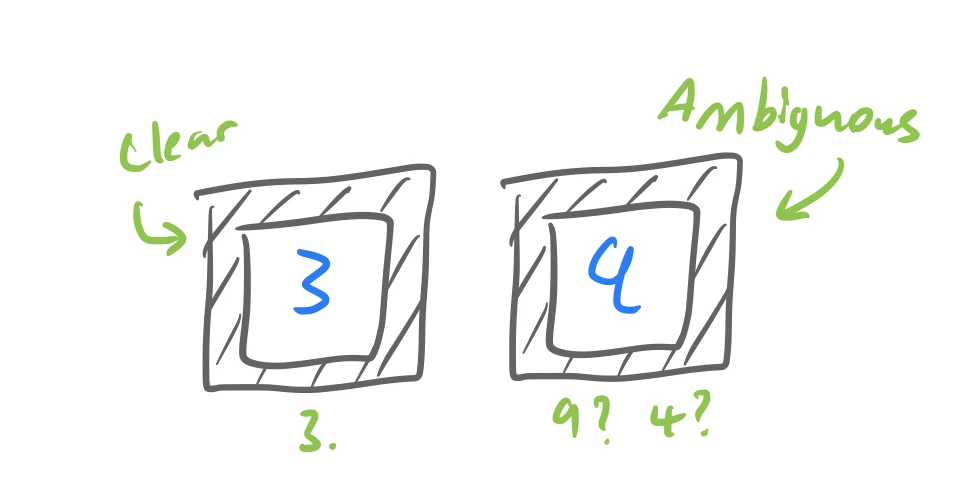
A great way to start to solve a question in science is to simplify the problem down to its basics. For instance, what if the dataset was only 10 digits? Then it would be easy, and we could do it without a computer just by looking at all the numbers ourselves and apply our own internal critique of what an ambiguous digit is. Perhaps these digits would be ones that we are not sure of what they are supposed to be? If we find them hard to classify¹ then they must be ambiguous, and we could just take the ones we find hardest to classify and use those as our ambiguous digits.

Great, now what if the dataset was 10,000 images? This is far too big for us to scan ourselves (would take over 14 hours non-stop with 5 seconds an image) but what if we got a machine to do it? We could then just take all the digits that it found hardest to classify and, just like us, if it found the digit hard to classify then surely it must be ambiguous.

Now all we need is a big dataset of handwritten digits and a machine that can classify them to test out our hypothesis!

The Dataset

For the dataset we can use the MNIST dataset which is a large collection of handwritten digits gathered by researchers in the late 90s numbering 70,000 digits total. Each digit has both is a 28x28 pixel greyscale image and the number of what the digit drawn was supposed to be. Assuming these labels are correct, we will call the label the ground truth from now on.

It is important that we have a dataset this large so that the computer can extract enough significant patterns from the data that generalise well. We do not want it to see ten different ways of drawing a 4, we want it to see thousands of different ways. This is so that it can extract the common elements which make a number four and what encodes its ‘fourness’. Learning this abstraction is the power of machine learning as it can then generalise to images that it has never seen before.

Making the Classifier

With the dataset found, next we need to create a machine that can classify handwritten digits. To do this we will use a convolutional neural network which is a specialised neural network designed to interpret images.

A convolutional neural network is a bunch of connected nodes that is loosely modelled on the neurons that our brain uses to work. The brain has billions of connections through its web of neurons, and if one fires then it can send a cascading ripple through its connected neurons like electricity through a wire. More specifically, the computer neural network aims to recreate how we see; from recognising edges of shapes then combining these to form whole objects and abstract constructions. While understanding exactly how it functions requires knowledge of linear algebra and coding, we can still gain a general idea of how it functions at a higher level.

The digit image is nothing more, to the computer, than a matrix (2-dimensional grid of numbers) of brightness levels of the pixel corresponding to that location as they are greyscale images. So, the input of the network must be a 28x28 matrix. However, the network does not recognise any aspects of the image yet and so to gain a higher order understanding of what the matrix encodes, we need to extract features from it.

Firstly, the network looks over the matrix and records what it sees for each pixel and those surrounding it like a magnifying glass. This is our first layer of feature extraction. Often the first layer detects very basic elements from the image such as edges of shapes and directions of these edges since as these can be seen using just a few pixels. More complex parts of the images cannot be recognised since they require more pixels to understand and the magnifying glass zooms in so much. This is then saved into a new matrix and known as the first convolution.

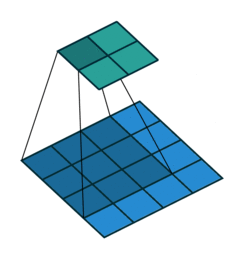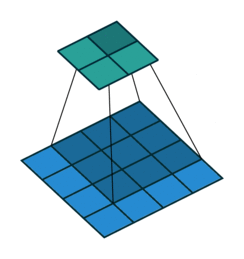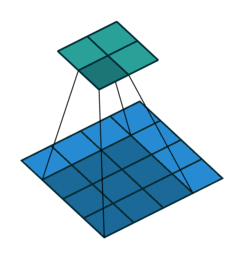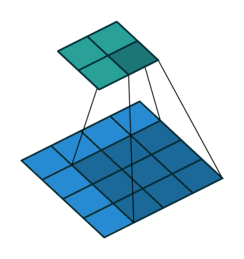
Secondly, this process is repeated but one generalisation higher. The network then looks over the first convolution’s output with a magnifying glass and then gains another level of feature extraction. Edges extracted in the first convolution can be matched with other edges to form curves, loops and more complex shapes. For instance, now the network could detect the “c” parts of a 3 and 5, as well as long straight lines corresponding to 1. The output of this second feature extraction is the second convolution.

It turns out this process can be repeated as many times as we want, but after the third convolution the generalisation has become so abstract that there is enough information in the output is to work out the digit. So the output of the convolutional neural network is fed into a traditional neural network to connect all the different abstractions together and form a comprehensive view of the image. This is done with two dense layers of fully connected neurons; an exact copy of how our brain works.

This is very well illustrated in the above diagram with a few convolution layers in the feature learning section and the dense layers in the classification section. The other layers such as Relu and (Max) Pooling are used to support the convolutional layer’s performance with a SoftMax used on the final layer so that the total probability is normalised to 1, but these are not essential to understand and isn’t where the magic happens anyway.

Coding the classifier

We can then code this model using Keras in Python and create the following summary of the network.

• The first two pairs of layers are the convolutional layers as discussed above
• The Flatten layer is simply to reduce the dimension from 2D to 1D
• The Dropout layer randomly drops some values. This is surprisingly useful as it minimises the delusions of the model and forces it to rely on multiple indicators instead of just one
• Finally there are two Dense layers the last having just 10 neurons. Whichever neuron has the highest value is the models’ prediction! (They are all normalised to sum to 1, so each can be thought of as the probability for being that digit).

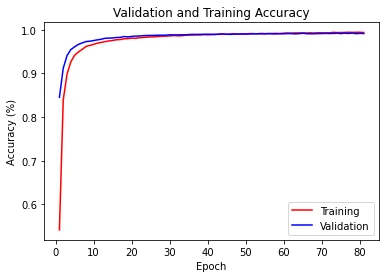
Putting this network to the test, we can train it on one part of the dataset and then test how well it performs on the other part that it has never seen before. Doing so gives promising results with an accuracy of 99.26% and a minimal loss of only 0.0285². For reference this took 48 seconds to train and is as good as the average human as we shall soon see. Now we can attempt to find the most ambiguous digits in the dataset.

Putting it all together

We’re now in an uncommon situation for machine learning that we both have a model that can predict digits and all the ground truth results for each digit. This is how we’re able to extract information from the model about which digits are ambiguous. Let’s come up with two definitions for ambiguity that we can use

1. A digit is ambiguous if the model is unconfident with its prediction.
2. A digit is ambiguous if the model is extremely confident with its prediction but is wrong.

Definition 1

A digit is ambiguous if the model is unconfident with its prediction.

To find these unconfident digits we can simply get the model to predict every image and record the value of its probability for its prediction. Then the digits with the lowest probability overall will correspond to the digits in the dataset that the model is the least confident with.

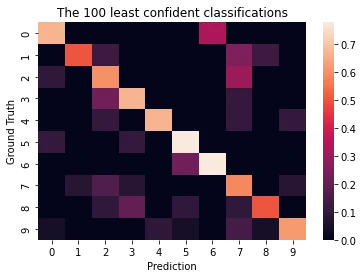
The least confident digits are shown in the heatmap above. The main diagonal is when the model’s prediction matched the ground truth of the digit. It is interesting to note that even for the network’s unconfident predictions it often still got it right.

Other light squares off the diagonal show where the network makes common mistakes. For instance, it appears to commonly confused twos and sevens as well as predict six when it really was a zero (interesting the converse isn’t true). Both are understandable since these digits do look similar.

What do some of these digits look like? Are they actually ambiguous?

Definitely ambiguous.

The digits’ titles are formed from the 4-digit code of digits’ index, inside the brackets is the network’s prediction first compared towards the ground truth. They are listed in increasing order of confidence.

The fact that the network is getting many of these results incorrect makes sense; it was unconfident about this prediction in the first case and so it knew it would have a high chance of getting the prediction wrong. As a human (sorry I’m not an AI) I agree with the model’s predictions except for 1182, 1522, 9664 and 247. Digit 4761 completely stumps me; I’ve no idea how that is supposed to be a nine…

So this definition was a success! What about the other?

Definition 2

A digit is ambiguous if the model is extremely confident with its prediction but is wrong

To find these digits we can simply do the reverse of the above, but throw away all digits that the model predicted correctly. We’re left with a selection of digits as follows.

These are even more ambiguous than before!

Most of these digits are weird, and I can see why it got most of them wrong. Consider digit 2130, this looks like a nine at first glance however the top isn’t joined. Perhaps it was supposed to be a four then? Digit 9729 could be a six with a scribble at the end or a five that accidentally joins at the bottom. Digit 3422 could go either way between zero and six depending on your interpretation of the bump at the top…

These different potential interpretations of what the digits are is exactly the definition of ambiguity. Not digits that are impossible to classify like 4176 and 2118, but digits that could really be classified easily two ways.

So while our definitions raises some false positives, there are so few that we can manually search through them to find the truly ambiguous digits in the dataset.

Afterword

The old days of only being able to process a dataset by Excel are gone, and instead we can now use computer’s themselves to learn the patterns of the data and find where they trip up.

This technique could be applied to numerous fields, and it allows us to quickly find information out about a dataset that in the past only stood out to a human. The applications are vast and mostly unthought of.

If you’re interested all the code is publicly accessible and available here.

Questions

Q: How do we know the labels for these ambiguous digits were done correctly? Perhaps they made a mistake, and it was only meant to be a scribble?

A: Perhaps, but even if it was a scribble then we have identified the digits that are certainly ambiguous even if they were not intended to be digits.

Q: If the dataset has been partitioned into ‘Train’ and ‘Test’ partitions, then surely the model will be more familiar with digits in the ‘Train’ partition and so the ambiguous digits will be biased towards the ‘Test’ partition that it is unfamiliar with?

A: Great question, I only searched for ambiguous digits in the ‘Test’ partition. As this contained 10,000 digits it was enough to find some really weird digits.

Q: Can you run the model backwards? Say if you wanted a four, could you set the output to four and then reverse it to extract an image of supreme “Fourness”?

A: Not really. Unfortunately neural network models are only really designed to be run in one direction. Theoretically it is possible (this is exactly what generative models do in fact) but we would have to change the layers to be ones that have a defined reversible function.

References

• Convolution image https://github.com/vdumoulin/conv_arithmetic
• MNIST dataset image https://en.wikipedia.org/wiki/MNIST_database
• MNIST dataset http://yann.lecun.com/exdb/mnist/

Futher Reading

• What is a Convolutional Neural Network? https://towardsdatascience.com/a-comprehensive-guide-to-convolutional-neural-networks-the-eli5-way-3bd2b1164a53
• Excellent book by the author of Keras to learn more about machine learning with Python https://www.manning.com/books/deep-learning-with-python